 |
Web www.pumpfundamentals.com |
 |
Web www.pumpfundamentals.com |
To size a pump or determine its total head, a calculation of the amount of fluid friction is required. Viscosity is the fluid property responsible for friction. The following is a brief discussion of viscosity.
VISCOSITY
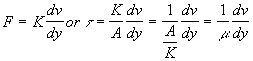 |
(A-1) |
The constant (A/K) is called the viscosity of the fluid and is represented by the Greek letter m (mu). The value of m will determine the magnitude of the shearing force (F). Fluids with higher viscosities will require a greater shearing force for the same velocity differential. Since the experiment should be valid for fluid bodies of any size, the tangential stress (t = F/A) is a more appropriate parameter to relate to viscosity.

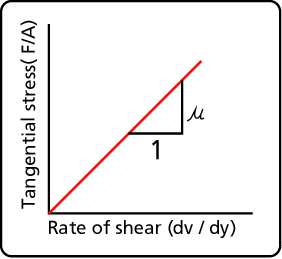
The term m is known as the absolute viscosity of the fluid (see equation A-l). The velocity gradient dv/dy is known as the rate of shear. Newton could not test his hypothesis because of experimental difficulties. Many years later, Poiseuille (1849) developed an experimental method that consisted in measuring the flow of liquid in a small tube and relating the pressure driving the fluid through the end of the tube to the flow and viscosity. Poiseuille's experimental apparatus verified the correctness of Newton's hypothesis. Newton's viscosity equation describes a class of fluids that came to be known as Newtonian fluids. Many fluids behave in this fashion (see Table A-2). The unit of absolute viscosity is the Poise (or centiPoise), in honor of Poiseuille. One (1) centiPoise (the unit symbol is cP) is the viscosity of water at 68 0F making it easy to compare the viscosity of various fluids to that of water.
NEWTONIAN VS. NON NEWTONIAN FLUIDS
The term m is known as the absolute viscosity of the fluid (see equation [A-1]). The velocity gradient dv/dy is known as the rate of shear. Newton could not test his hypothesis because of experimental difficulties. Many years later, Poiseuille (1849) developed an experimental method that consisted in measuring the flow of liquid in a small tube and relating the pressure driving the fluid through the end of the tube to the flow and viscosity. Poiseuille's experimental apparatus verified the correctness of Newton's hypothesis. Newton's viscosity equation describes a class of fluids that came to be known as Newtonian fluids. Many fluids behave in this fashion (see Table A-2). The unit of absolute viscosity is the Poise (or centiPoise), in honor of Poiseuille. One (1) centiPoise (the unit symbol is cP) is the viscosity of water at 68 0F, making it easy to compare the viscosity of various fluids to that of water.
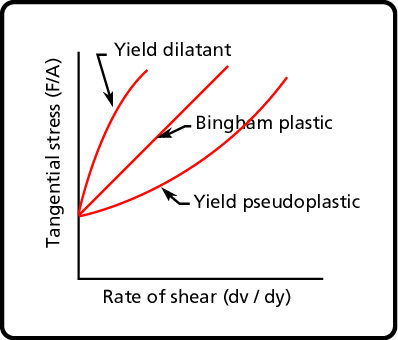
Many fluids do not behave in the well-ordered fashion of Newtonian fluids. These are known as non-Newtonian fluids and fall in several categories (see Table A-2) depending on what shape the tangential stress vs. velocity gradient takes. For these fluids, the viscosity is variable. In the literature, a variable viscosity is often referred to as apparent viscosity. The velocity gradient affects the viscosity, resulting in a much higher (or in some cases lower) tangential stress than for a Newtonian fluid.
A typical household product will help illustrate this point. Try the following experiment. In a large shallow bowl make a solution of approximately 1 part water and 2 parts cornstarch, try moving this fluid rapidly around with your fingers. When the fingers are moved slowly, the solution behaves as expected, offering little resistance. The faster you try to move through the fluid, the higher the resistance. At that rate of shear, the solution almost behaves as a solid, If you move your fingers fast enough they will skip over the surface. This is what is meant by viscosity being dependent on rate of shear. Compare this behavior to that of molasses; you will find that even though molasses is viscous its viscosity changes very little with the shear rate. Molasses flows readily no matter how fast the movement.
This explains why centrifugal pumps with their high rate of shear are not suitable for non-Newtonian fluids. A pump of the fixed displacement type, operating at low speed, is more appropriate.
Kinematic viscosity
A term frequently used in fluid mechanics (for example in the definition of the Reynolds number) is the kinematic viscosity n . The relationship between the absolute and kinematic viscosity is:
| NEWTONIAN |
|
||||
| Non Newtonian | Bingham plastic
Yield pseudoplastic Yield dilatant |
Pseudoplastic | Dilatant | Thixotropic
Rheopectic |
|
|
 |
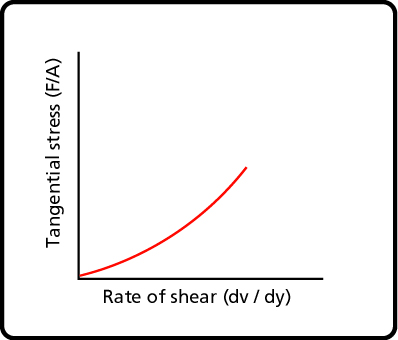
Viscosity decreases with the rate of shear. |
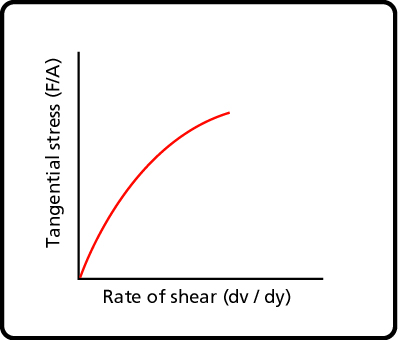
Viscosity increases with the rate of shear. |
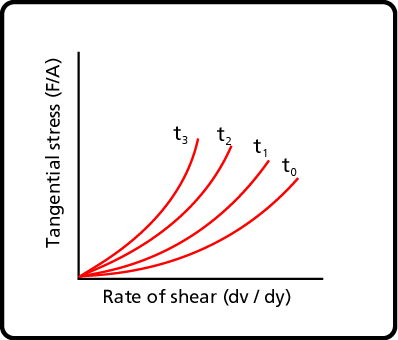
Thix.: decrease viscosity with time. Rheop.: increase viscosity with time. |
|
| - water
- high viscosity fuel - some motor oils - most mineral oils - gasoline - kerosene - most salt solutions in water - light suspensions of dye stuff - kaolin (clay slurry) |
oils containing polymeric thickeners, viscosity index improvers and waxy or soot particles | - thermoplastic polymer solutions
- sewage sludge’s - digested sewage> - clay - mud - ketchup - chewing gum - tar - high concentrations of asbestine in oil |
- GRS latex solutions
- sewage sludge’s - grease - molasses - paint - starch - soap - most emulsions - printer’s ink - paper pulp> |
- starch in water
- beach sand - quicksand - feldspar - mica - clay - candy compounds - peanut butter |
- most paints (thixo.)
- silica gel - greases - inks - milk - mayonnaise - carboxymethyl cellulose - bentonite (rheop.) - gypsum in water - asphalt - glues - molasses - starch - lard - fruit juice concentrates |
Table A-2 Rheological properties of Fluids
Copyright 2019, PumpFundamentals.com